Al ver la hoja
de características técnicas del micrófono
noté que era de alta impedancia, recomendando
el fabricante la utilización de un buffer
o adaptador para pasar de alta a baja impedancia.
Estos aparatitos son comunes en las guitarras acústicas,
que utilizan este tipo de micrófonos también,
son unas cajitas que tienen además de volumen
un control de tono y que están a mano del
músico. Como es costumbre, como no había
en plaza un preamplificador de este tipo, lo diseñé
sobre la base de un ecualizador a giradores y se
los ofrezco en estas páginas, por si les
toca fabricar uno o en el caso de encontrar un ecualizador
parecido que deban reparar, para comprender cómo
funciona.
LOS GIRADORES:
Veamos el circuito de la figura 1. Allí tenemos
una capacidad en serie con una inductancia puesta
a masa, conformando un circuito resonante serie.
Si barremos la entrada de este circuito con un generador
de frecuencias notaremos que a f0 (la frecuencia
de resonancia del circuito resonante) la salida
disminuye. En el caso de los preamplificadores de
audio elegiremos los valores de L y C para que resuenen
en una frecuencia de audio. Podemos entonces ver
cómo funciona un elemental control de tono
con este sistema.
Analicemos el caso de la figura
2. Aquí tenemos el sistema LC en la entrada
no inversora del amplificador operacional, por lo
que a la salida obtenemos una disminución
de la ganancia en la frecuencia de resonancia del
filtro, al derivar éste a masa esas frecuencias,
en este caso tenemos un atenuador selectivo.
En la figura 3, por el contrario,
el filtro LC está en la entrada inversora
del operacional, produciendo el efecto contrario
al ejemplo anterior, aumentando la salida en la
frecuencia de resonancia del sistema LC. ¿Por
qué sucede esto? Si recuerdan una de las
máximas del amplificador operacional es que
entre las entradas inversora y no inversora la diferencia
de potencial el cero. A la frecuencia de resonancia
del filtro LC llega menos tensión proveniente
de la salida a la entrada inversora, dado que la
red LC la deriva a masa. Para compensar esto el
operacional eleva su tensión de salida para
equilibrar esta pérdida de tensión
y mantener la condición V+ = V-. Como vemos
en este caso, la ganancia del operacional se hace
selectiva a la frecuencia, en este caso a la de
resonancia del filtro LC. Si ponemos varios filtros,
uno para las frecuencias graves, otro para las medias
y otro para las agudas, seleccionándolos
por medio de potenciómetros, que deriven
el filtro a la entrada inversora (para amplificar)
y la no inversora (para atenuar) obtendremos un
control de tono como el de la figura 4.
Aquí nos encontramos con
un pequeño inconveniente: las inductancias
para un filtro LC para el rango de audio tienden
a ser grandes, del orden de las decenas de milihenrios,
lo que las hace voluminosas y difíciles de
conseguir, por lo que se las simula electrónicamente
con un circuito que se denomina girador, denominado
así porque hace que una reactancia capacitiva
se vea como una inductiva. Recordemos que la reactancia
capacitiva se expresa como 1/j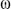 C,
representándose con una flecha para abajo,
mientras que la reactancia inductiva se expresa
como j C,
representándose con una flecha para abajo,
mientras que la reactancia inductiva se expresa
como j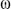 L,
y se representa como una flecha para arriba. El
hecho de hacer “girar” la flecha desde
abajo (capacitiva) hacia arriba (inductiva) es lo
que le da el nombre a este dispositivo, del que
tenemos uno para estudio en la figura 5. L,
y se representa como una flecha para arriba. El
hecho de hacer “girar” la flecha desde
abajo (capacitiva) hacia arriba (inductiva) es lo
que le da el nombre a este dispositivo, del que
tenemos uno para estudio en la figura 5.
Una vez comprendido el concepto vamos a ver su desarrollo
matemático. Para ello simplificamos las ecuaciones
dando los siguientes presupuestos: A) la impedancia
de entrada del operacional es infinita Zin=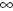 .
B) la ganancia de tensión del operacional
es infinita .
B) la ganancia de tensión del operacional
es infinita 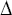 V= V=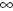 .
C) la impedancia de salida del operacional es cero
Zout=0. Podemos ir presentando una serie de ecuaciones: .
C) la impedancia de salida del operacional es cero
Zout=0. Podemos ir presentando una serie de ecuaciones:
(V1-V2) / R3 = I2 (1)
(V1-V3) / R2 = I4 (2)
(V1-V3) / R1 = I1 (3)
Como Zin = 0 Iin = 0 por lo tanto:
I2 = I4 y Iin = I1
Según la ecuación
(3) (V1 – V3) = I1 . R1; pero como I1 = Iin
se puede igualar:
V1 – V3 = Iin . R1
Si dividimos ambos miembros por
R2 obtenemos las siguientes ecuaciones
(V1 – V3) / R2 = (Iin . R1)
/ R2 (4)
Al ser I2 = I4 se pueden igualar
las ecuaciones (1), (2) y (4), obteniendo:
(V1 – V2) / R3 = (V1 –
V3) / R2 = (Iin . R1) / R2
Si analizamos el circuito podremos
ver que:
(V1 – V2) = I3 / j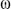 C C
observemos que en este punto la
reactancia es capacitiva = 1/j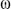 C
Si substituímos I3 por su equivalente V1
/ R4 tenemos: C
Si substituímos I3 por su equivalente V1
/ R4 tenemos:
(V1 – V2) = V1 / j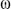 C
R3 R4 C
R3 R4
podemos ver que el primer miembro
de la ecuación es igual a la ecuación
Nº4, por lo que podemos escribir:
(R1 . Iin) / R2 = V1 / j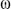 C3 R4
C3 R4
si multiplicamos en cruz obtenemos:
j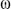 C R1 R3 R4 Iin = V1 R2 (5) pero tenemos que V1 =
Vin, y la impedancia de entrada es Zin = Vin / Iin
por lo que utilizando la ecuación (5) tenemos:
C R1 R3 R4 Iin = V1 R2 (5) pero tenemos que V1 =
Vin, y la impedancia de entrada es Zin = Vin / Iin
por lo que utilizando la ecuación (5) tenemos:
Zin = Vin / Iin = V1 / Iin = (j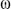 C R1 R3 R4) / R2
C R1 R3 R4) / R2
Notemos que aquí la reactancia
pasó a ser inductiva, (+j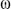 ).
Es aquí donde se produce el efecto girador.
Podemos escribir L = (C R1 R3 R4) / R2 y si hacemos
todas las resistencias iguales tenemos L = C R ).
Es aquí donde se produce el efecto girador.
Podemos escribir L = (C R1 R3 R4) / R2 y si hacemos
todas las resistencias iguales tenemos L = C R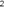 . .
En la figura 6 tenemos la plaqueta
de circuito impreso y en la figura 7 la disposición
de los componentes. El circuito se debe alimentar
con una batería de 9 Volts, y la duración
de la misma (una alcalina) es de aproximadamente
unas 20 horas. Recuerden conectar el positivo de
la batería a la pata 8 del CI y el negativo
a la pata 4.
|